Normative Musicology: Automatic Tonal Induction via Entropy and Rational Expectation

A new branch of systematic musicology, “normative musicology,” is proposed and its practice demonstrated. Normative musicology is the study of optimal (“norma-tive”) expectations about future musical signals, given some corpus of past signals. It is a formalization of many “statistical learning” approaches (e.g. [1]) and may be considered a computational counterpart to empirical musicology. It is shown that a broad spectrum of music analyses and theories can be formulated as hypotheses about expectations, and thus may be tested with normative musicology. 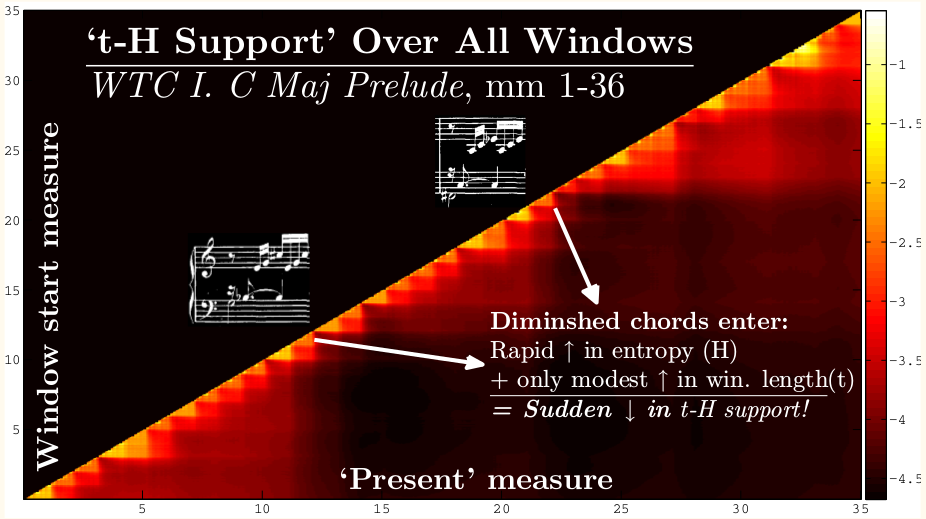The practice of normative musicology is, in essence, the unsupervised extraction of musical features invariant to certain transformations, consistent with “transfor-mational” [2] and geometric [3, 4] music theories. An example of the practice of normative musicology is presented: two pitch distributions, invariant to translations in a reference pitch (“tonic”) and time, are naturally “perceived” in J.S. Bach’s Well-Tempered Clavier by an unsupervised learning algorithm; these closely match empirically determined major and minor “key profiles” [5]. Furthermore, a two-dimensional geometric mapping of all translation distances, performed using multi-dimensional scaling, yields the familiar “circle of fifths,” while a three-dimensional mapping reveals, albeit more ambiguously, the helical structure suggested by [3]. We conclude by proposing a generic algorithm for normative music analysis, based on shift-invariant probabilistic latent component analysis [6]. References [1] Marcus T. Pearce and Geraint A. Wiggins. Expectation in melody: The influ-ence of context and learning. Music Perception: An Interdisciplinary Journal, 23(5):377–405, 2006. [2] David Lewin. Generalized musical intervals and transformations. Oxford Uni-versity Press, 2007. [3] Elaine Chew. Towards a mathematical model of tonality. PhD thesis, Mas-sachusetts Institute of Technology, 2000. [4] Dmitri Tymoczko. A geometry of music. New York: Oxford University Press, 2011. [5] Carol L Krumhansl. Cognitive foundations of musical pitch, volume 17. Oxford University Press New York, 1990. [6] Paris Smaragdis and Bhiksha Raj. Shift-invariant probabilistic latent component analysis. Journal of Machine Learning Research, 2007.